Monte Carlo Simulation of 2D Ising Model

• Introduction
• The Ising Model
• Monte-Carlo Simulation
  • Physical Model
  • Python Implementation
    • Python code for Ising model
• Results
• Reproduction
• Appendix
  • Results
    • python 3.11
    • python 3.10
    • python 3.9
    • python 3.8
    • Other versions

Introduction

During my first year PhD at UC, I get the chance to take statistical mechanics class from a condensed matter physicist. It was a new experience when he focused too much on different side that I did not explore before. The final project in this class was about using Monte-Carlo method to simulate the Ising model. Ising model is a model of a system that undergoes a phase transition. There are many reasons why this model is interesting when it is not representing any actual physical systems.

1. It can be solved exactly, We can calculate the thermodynamical quantities and interpret them. In another can calculate the partition function and put it in an exact form.
2. Ising model exhibits symmetry breaking in low-temperature phase.
3. It is a simple model that can be used to understand the physics of phase transition.
4. The Ising model is simple, yet it can be applied to many physical systems. This gives us a feature about universality, a feature that tells us that in such case the same theory applies to all sorts of different phase transitions.

The Ising Model

We can think of Ising model as a mathematical model where everything consists of small squares inside a bigger one. It is usually called lattices where we then have a big lattice of sites (small boxes) where each site can be in one of two states. Those states as we will see will refer to the spin state of the electron inside this site. Each site will be labeled by index ii. The Hamiltonian for the Ising model can be written as

$$\mathcal{H}=-J \sum_{\langle i j\rangle} S_i S_j$$

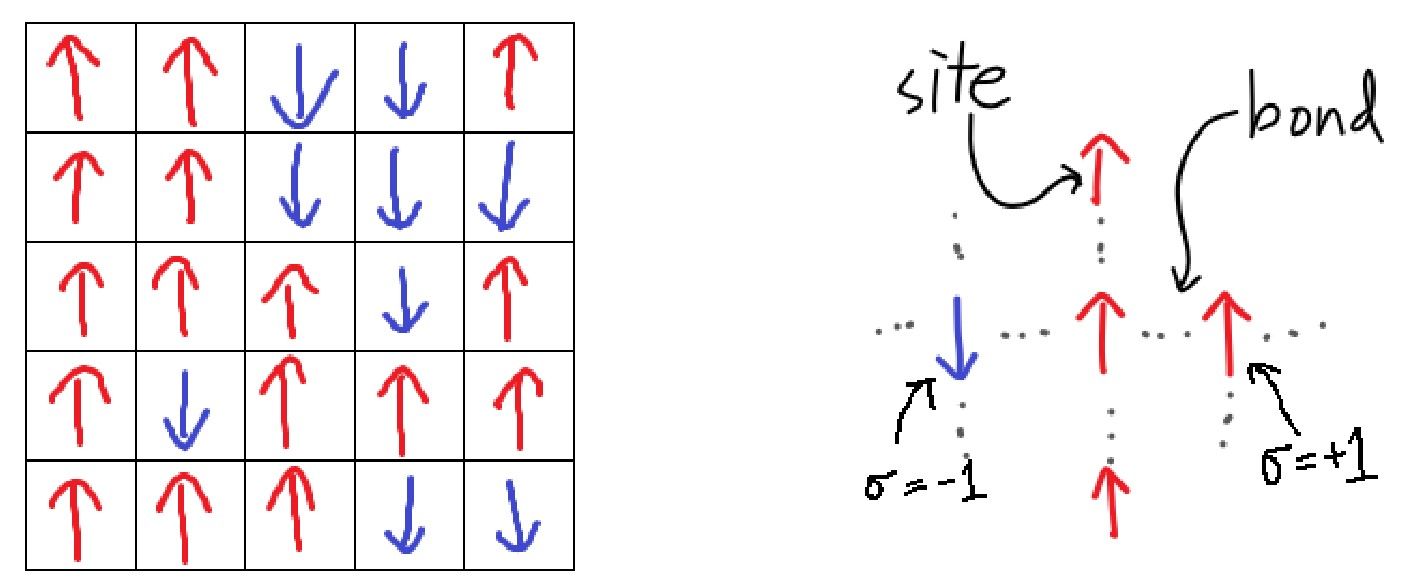
There are many systems that can be represented using this model like “lattice gas” with each of the sites is the possible location of a particle; means that site is empty and means that site is occupied by a particle.

This system will undergo a 2nd order phase transition at some temperature $$T=T_c$$ which is called critical temperature. For cases when $$T < T_c$$, the system magnetizes, and the state is called the ferromagnetic state which is an ordered state. For cases when $$T > T_c$$ ​, the system is disordered or in a paramagnetic state. We can define the order parameter for this system to be the average magnetization $$m$$.

This parameter is used to distinguish between the two phases that this system can have. It is zero when we are in disordered (paramagnetic) state and takes a non-zero value in ordered (ferromagnetic) state.

Monte-Carlo Simulation

In this section, I’m going through the details of implementing the Monte-Carlo (MC) method for our Ising model. I apply the MC methods using Metropolis Algorithm to Ising model and extract physical parameters (Energy, Specific heat and Magnetization).

Physical Model

Lattice is a periodical structure of points that align one by one. 2D lattice can be plotted as:

1* * * * * * * *   
2* * * * * * * * 
3* * * * * * * *
4* * * * * * * *
5* * * * * * * *

The points in lattice are called lattice points, nearest lattice points of point ^ are those lattice points denoted by (*) shown in the graph below:

1* * *(*)* * * *
2* *(*)^(*)* * *
3* * *(*)* * * *
4* * * * * * * *

Each lattice point is denoted by a number i in the Hamiltonian.

The expression for the Energy of the total system is

1* * * * * * * * 
2* * * * * * * *
3* * * * * * * * <-the i-th lattice point
4* * * * * * * *
5* * * * * * * *

Periodical structure means that lattice point at(1,1) is the same as that at(1,9) if the lattice is 5 x 8. For example (1,1)<=>(6,1), (2,3)<=>(2,11). A 2D lattice can be any $$N_x$$ by $$N_y$$ . The location $$(x,y)$$ here is another denotion of lattice point that is fundamentally same as i-th lattice point denotation above.

1* * * * * * * * 4
2* * * * * * * * 3
3* * * * * * * * 2
4* * * * * * * * 1
51 2 3 4 5 6 7 8 

Python Implementation

The metropolis algorithm steps can be written as the following steps:

1. Prepare some initial configurations of N spins.
2. Flip spin of a lattice site chosen randomly
3. Calculate the change in energy due to that flip
4. If this change is negative, accept such move. If change is positive, accept it with probability$$ex{p}^{-dE⁄kT}$$
5. Repeat 2-4.
6. Calculate physical properties such as Energy, Specific heat and Magnetization
7. optional plot the physical properties as a function of temperature

Lets try to implement this algorithm in python. We start by importing the necessary libraries. We use numpy for array and matrix operations, matplotlib for plotting, numba for faster computation and random for random number generation. We use tqdm for progress bar and time module to test the speed of the algorithm. If we are using jupyter notebook, we can use tqdm.notebook for progress bar.

1import matplotlib.pyplot as plt
2from numba import jit 
3import numpy as np 
4import random 
5import time 
6from tqdm import tqdm 

First thing we need to do now is to define the system paramerters. We need to initialize the spin configuration, the temperature range and the number of MC sweeps. Also we are assuming that we have a square lattice of size L x L and that there is no external magnetic field. We define spin s and initialize it with random values (+1 or -1) for up or down spins. We also define the number of MC sweeps n and the temperature range Temperature. The purpose of sweeps is to equilibrate the system to the desired temperature.

1B = 0; # Magnetic field strength
2L = 50; # Lattice size (width)
3s = np.random.choice([1,-1],size=(L,L)) # random spin sites with values (+1 or -1) for up or down spins. 
4n= 1000 * L**2 # number of MC sweeps 
5Temperature = np.arange(1.6,3.25,0.01) # Temperature range, takes form np.arange(start,stop,step)

I usually prefer functional programming and have everything in functions to make the code more readable. So I define functions to compute the energy and magnetization of the lattice. Lets start by implementation a function to calculate the energy of the lattice. The function will take the spin configuration as input and return the energy of the lattice. We calculate the energy as the sum of interactions between spins divided by the total number of spins.

 1'''
 2Energy of the lattice calculations. 
 3The energy is the sum of interactions between spins divided by the total number of spins
 4'''
 5
 6@jit(nopython=True, cache=True) 
 7def calcE(s):
 8    E = 0
 9    for i in range(L):
10        for j in range(L):
11            E += -dE(s,i,j)/2
12    return E/L**2
13 

Next we implement a function to calculate the magnetization of the lattice. The function will take the spin configuration as input and return the magnetization of the lattice. We calculate the magnetization as the sum of all spins divided by the total number of spins.

1'''
2Calculate the Magnetization of a given configuration
3Magnetization is the sum of all spins divided by the total number of spins
4'''
5@jit(nopython=True, cache=True) 
6def calcM(s):
7    m = np.abs(s.sum())
8    return m/L**2

What we need now is to write a function that will calculate the change in energy due to a spin flip.

 1
 2'''
 3# Calculate interaction energy between spins. Assume periodic boundaries.
 4# Interaction energy will be the difference in energy due to flipping spin i,j 
 5# (Example: 2*spin_value*neighboring_spins)
 6'''
 7
 8@jit(nopython=True, cache=True) 
 9def dE(s,i,j): # change in energy function
10    #top
11    if i == 0:
12        t = s[L-1,j]  # periodic boundary (top)
13    else:
14        t = s[i-1,j]
15    #bottom
16    if i == L-1:
17        b = s[0,j]  # periodic boundary (bottom)
18    else:
19        b = s[i+1,j]
20    #left
21    if j == 0:
22        l = s[i,L-1]  # periodic boundary (left)
23    else:
24        l = s[i,j-1]
25    #right
26    if j == L-1:
27        r = s[i,0]  # periodic boundary  (right)
28    else:
29        r = s[i,j+1]
30    return 2*s[i,j]*(t+b+r+l)  # difference in energy is i,j is flipped

Now that we have implemented the functions that will do the calculations. We need to implement the Monte-carlo sweep. The idea is to start by choosing a random lattice site and flip its spin. Then we calculate the change in energy and accept the change with probability $$ex{p}^{-dE⁄kT}$$. If the change is not accepted, we repeat the process with a new spin configuration.

 1# Monte-carlo sweep implementation
 2@jit(nopython=True, cache=True) 
 3def mc(s,Temp,n):   
 4    for m in range(n):
 5        i = random.randrange(L)  # choose random row
 6        j = random.randrange(L)  # choose random column
 7        ediff = dE(s,i,j)
 8        if ediff <= 0: # if the change in energy is negative
 9            s[i,j] = -s[i,j]  # accept move and flip spin
10        elif random.random() < np.exp(-ediff/Temp): # if not accept it with probability exp^{-dU/kT}
11            s[i,j] = -s[i,j]
12    return s

We need to implement the function the calculate the physical properties of the system. The proprties that we will calculate are the energy, the specific heat and the magnetization. The function will take the spin configuration, temperature and number of sweeps as input. The functions will return the energy, specific heat and magnetization.

 1# Compute physical quantities
 2@jit(nopython=True, cache=True) 
 3def physics(s,T,n):
 4    En = 0
 5    En_sq = 0
 6    Mg = 0
 7    Mg_sq = 0
 8    for p in range(n):
 9        s = mc(s,T,1)
10        E = calcE(s)
11        M = calcM(s)
12        En += E
13        Mg += M
14        En_sq += E*E
15        Mg_sq += M*M
16    En_avg = En/n
17    mag = Mg/n
18    CV = (En_sq/n-(En/n)**2)/(T**2)
19    return En_avg, mag, CV

Now we are ready to use our functions to run the simulation. We need to initialize the variables that will store the results. mag will store the magnetization, En_avg will store the average energy and CV will store the specific heat capacity.

1# Inititalize magnetization, average energy and heat capacity
2mag = np.zeros(len(Temperature))
3En_avg = np.zeros(len(Temperature))
4CV = np.zeros(len(Temperature))

Up to this point everything is just defining functions and initializing variables. If we want to time the algorithm run then we don’t want to include the initialization part in the timing. So we will start the timer after we have initialized the variables.

1start = time.time()

Next step we write a for-loop that will run the simulation at each temperature and store the results. It loops over n and T and calls the physics function. Then we end the timer and print the time it took to run the code.

 1# Simulate at particular temperatures (T) and compute physical quantities
 2for ind, T in enumerate(track(Temperature)):
 3    # Sweeps spins
 4    s = mc(s,T,n)
 5    # Compute physical quanitites with 1000 sweeps per spin at temperature T
 6    En_avg[ind], mag[ind], CV[ind] = physics(s,T,n)
 7end = time.time()
 8print("Time it took in seconds is = %s" % (end - start))
 9time = (end - start)/60
10print('It took ' + str(time) + ' minutes to execute the code')

Now that we have run the simulation, we can plot the results. The plots will show the energy, specific heat and magnetization as a function of temperature.

 1f = plt.figure(figsize=(18, 10)); # plot the calculated values
 2sp =  f.add_subplot(2, 2, 1 );
 3plt.plot(Temperature, En_avg, marker='.', color='IndianRed')
 4plt.xlabel("Temperature (T)", fontsize=20);
 5plt.ylabel("Energy ", fontsize=20);         plt.axis('tight');
 6
 7sp =  f.add_subplot(2, 2, 2 );
 8plt.plot(Temperature, abs(mag), marker='.', color='RoyalBlue')
 9plt.xlabel("Temperature (T)", fontsize=20); 
10plt.ylabel("Magnetization ", fontsize=20);   plt.axis('tight');
11
12sp =  f.add_subplot(2, 2, 3 );
13plt.plot(Temperature, CV, marker='.', color='IndianRed')
14plt.xlabel("Temperature (T)", fontsize=20);  
15plt.ylabel("Specific Heat ", fontsize=20);   plt.axis('tight');   
16
17plt.subplots_adjust(0.12, 0.11, 0.90, 0.81, 0.26, 0.56)
18plt.suptitle("Simulation of 2D Ising Model by Metropolis Algorithm\n" + "Lattice Dimension:" + str(L) + "X" + str(
19    L) + "\n" + "External Magnetic Field(B)=" + str(B) + "\n" + "Metropolis Step=" + str(n))
20plt.show() # we save use plt.savefig('results.png') to save the plot

Results

I have ran the simulation for lattice dimension 50x50 and with metropolist steps of 2500000 and external magnetic field of 0.0. The results are shown below. We can play with different configurations and see how the results change.

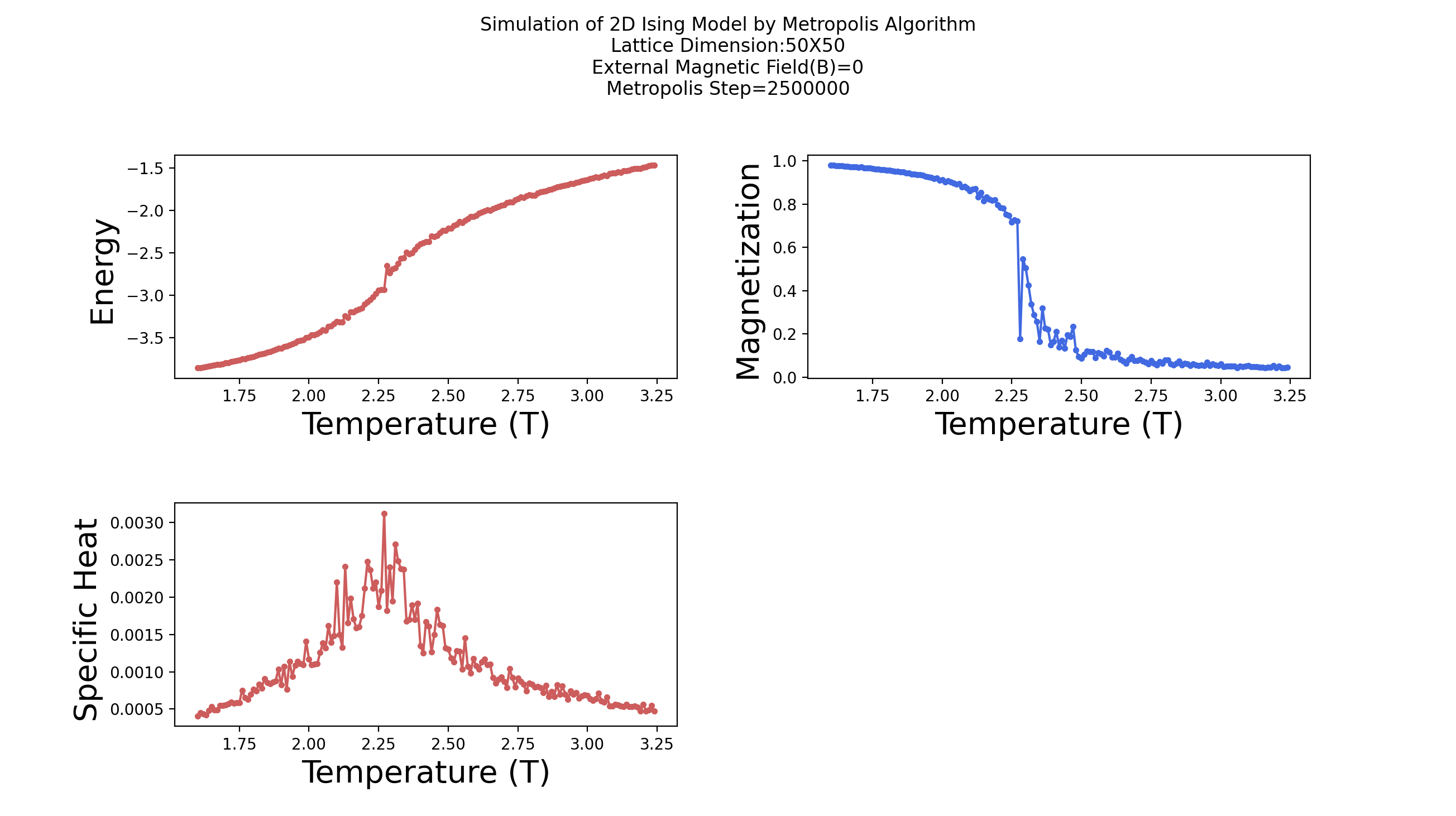
Reproduction

If you want to reproduce the results you can run the code on Colab, or you can download from GitHub repository and run locally. Also, there is python script that you can run. I’m using Numba cache so that it produces cache folder (specific to machine CPU and configuration) so that you will need to produce yours by running it for one time and subsequent runs will be about twice faster.

To run the script

1. clone the repository git clone https://github.com/MohamedElashri/IsingModel
2. run the script python IsingModel/IsingModel.py

Appendix

I have used this codebase as a benchmark test for python releases. I plan on maintain this test (available as repo on github). Initialy I used numpy-1.23.4 for all different version of python used in the benchmark. This is the latest version of numpy. I got the following results.

Results

The benchmarks are executed on Macbook pro Apple Silicon M1 version. The python versions are installed using homebrew

The arguments of the script are L(length of the lattice), n(number of Monte Carlo cycles).

python 3.11

1time python3.11 ising.py 10 10000
2Time it took in seconds is = 109.2954261302948
3python3.11 ising.py 10 10000  110.82s user 0.79s system 100% cpu 1:51.38 total

python 3.10

1time python3.10 ising.py 10 10000
2Time it took in seconds is = 123.83638191223145
3python3.10 ising.py 10 10000  124.80s user 0.69s system 101% cpu 2:04.06 total

python 3.9

1time python3.9 ising.py 10 10000
2Time it took in seconds is = 123.56476402282715
3python3.9 ising.py 10 10000  123.94s user 1.08s system 101% cpu 2:03.67 total

python 3.8

1time python3.8 ising.py 10 10000
2Time it took in seconds is = 135.1741383075714
3python3.8 ising.py 10 10000  137.05s user 1.00s system 100% cpu 2:17.24 total

Other versions

Python started supporting apple silicon starting from python3.8 and I try to make things as consistent as possible. Not to mention that numpy optimization for different version might be unaccounted difference.